Merge Sort(머지 소트)
2021. 8. 4. 22:48ㆍ알고리즘(Algorithm)
전형적인 divide-and-conquer알고리즘
퀵 소트의 분할된 크기에 따라 영향을 많이 받는 것을 막기 위한 방법
강제로 절반으로 나누어서 분할하는 방법
Merge Sort 코드


Merge Sort구현 방법
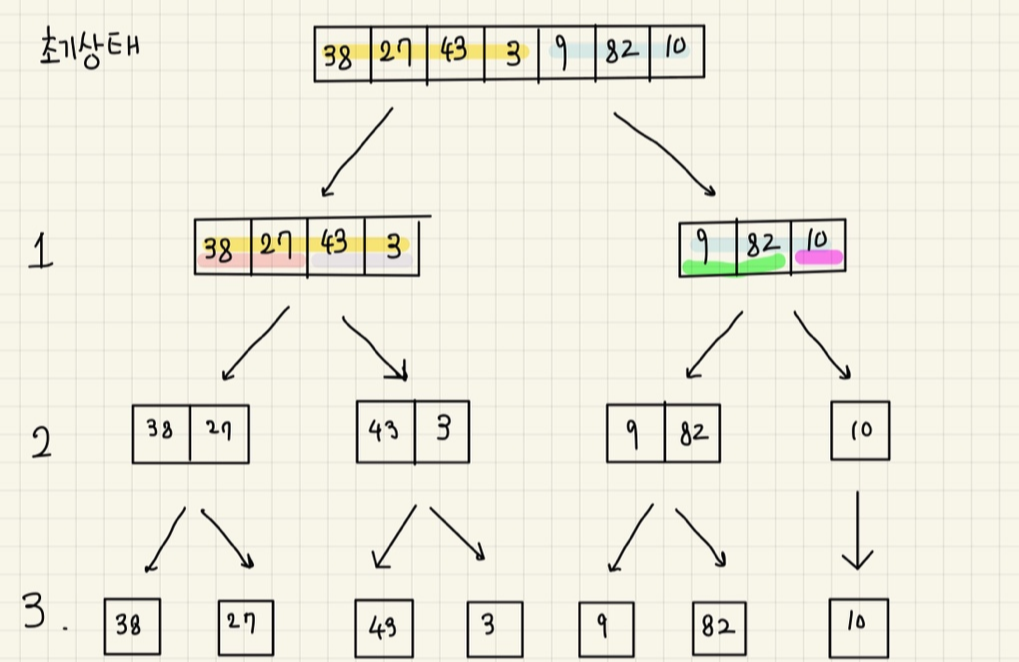
초기상태: 정렬이 필요한 list
1. (대략적인) 절반을 기준으로 나눈다(노랑&파랑)
2. 1번을 반복한다.
3. 모든 수가 각각 하나로 분리되었다.

4.
- 3에서 각각 분할 된 것을 정렬하여 합친다.
- 정렬 시, 둘 중 작은 것을 먼저 넣고, 둘 중 하나라도 끝나면 나머지는 그냥 모두 순서대로 넣는다.
5&6. 4번 과정처럼 병합 한다.
시간 복잡도
| n/2 | n/2 |
T(n) = 2*T(n/2) + (merge_two_sorted_lists)
= 2*T(n/2) + c*n
=O(nlogn)
언제 어디서든 어떤 데이터이든 절반으로 나누기 때문에 O(nlogn)이 보장(Worst Case, Best Case, Average Case모두)
특징
단점
- 만약 레코드를 배열(Array)로 구성하면, 임시 배열이 필요하다. not-in-place정렬이다
- 레크드들의 크기가 큰 경우에는 이동 횟수가 많으므로 매우 큰 시간적 낭비를 초래한다.
장점
- 안정적인 정렬 방법
- 데이터의 분포에 영향을 덜 받는다. 즉, 입력 데이터가 무엇이든 간에 정렬되는 시간은 동일하다. (O(nlog₂n)로 동일)
출처
https://gmlwjd9405.github.io/2018/05/08/algorithm-merge-sort.html
https://www.youtube.com/playlist?list=PLsMufJgu5932XYejsOwcUDJ2F75f56nrl
'알고리즘(Algorithm)' 카테고리의 다른 글
| Binary Search_이진탐색 (0) | 2021.08.10 |
|---|---|
| Insertion Sort(삽입 정렬) (0) | 2021.08.05 |
| Quick Sort(퀵소트) (0) | 2021.08.04 |
| Sorting(정렬) (0) | 2021.08.02 |
| 알고리즘 정의와 분석 방법 (0) | 2021.05.24 |